Introduction
智能体(Agent)是一个能够感知环境(Environment)中的状态(State)并采取动作(Action)的实体。智能体的目标是在某些时间步中,以最大化的总回报或奖励(Reward)完成任务。为了实现这个目标,智能体需要利用之前的经验和当前的信息来选择最佳的动作,这个选择过程根据策略(Policy)来执行。
- Agent:智能体,它是一个能够在环境中执行操作(动作)的实体,其目标是获得最大化的回报(reward)。
- Environment:环境,它是智能体所处的场景,包括所有的状态(state)、动作(action)、奖励(reward)和转移规则(transition rules)等。
- Policy:策略,它是智能体决策的过程,将当前状态映射到要采取的动作的概率分布。
- Action:动作,它是智能体在环境中执行的行为或操作。
- Reward:奖励,它是表示智能体行为良好或不良的量化反馈值。在强化学习中,智能体的目标是最大化长期的回报(累积奖励)。
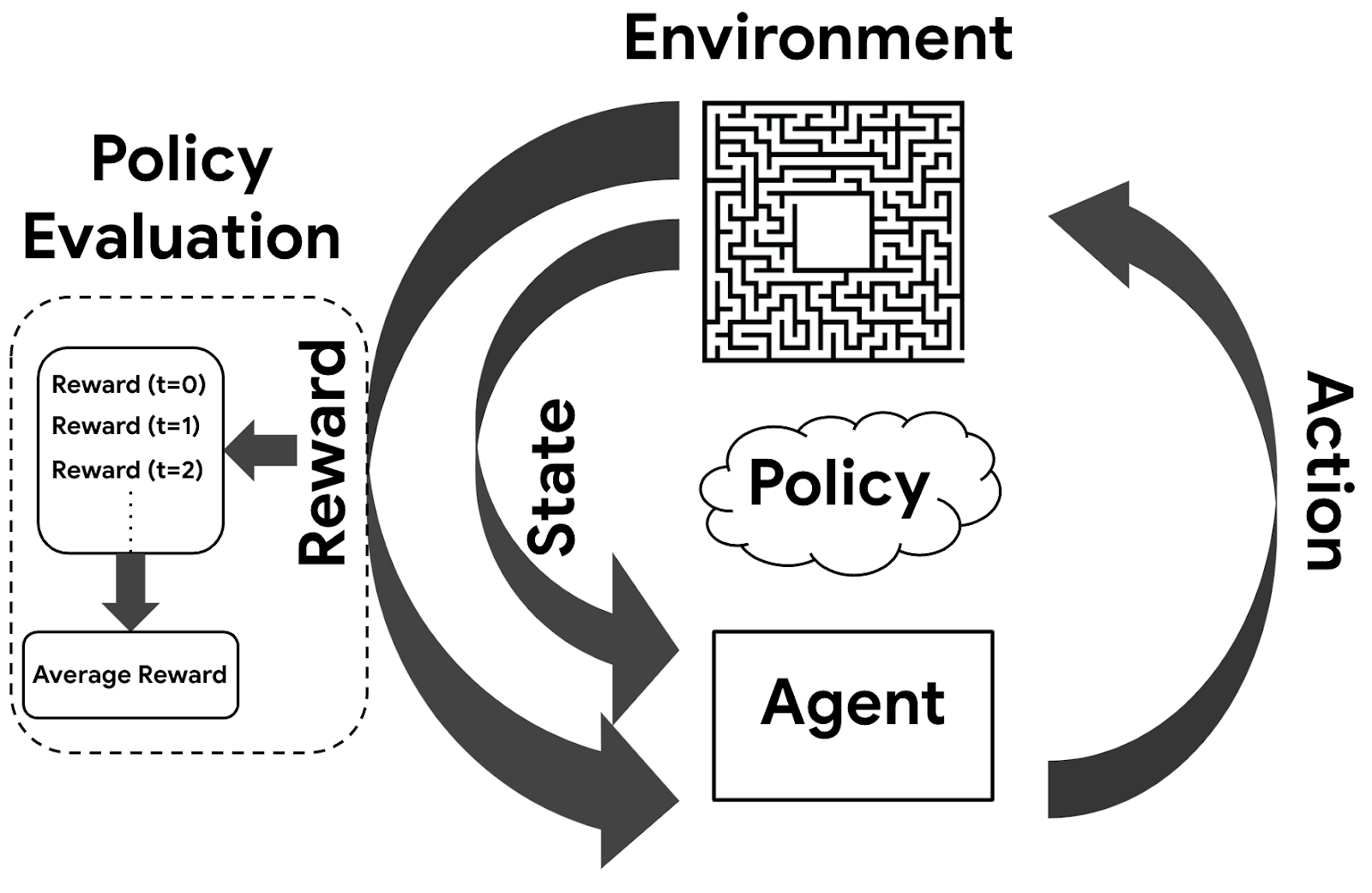
Key Concepts
如何将上述过程抽象为数学过程呢,首先介绍几个比较重要的概念:回报函数(Reward Function),状态价值函数(State-Value Function)以及动作价值函数(Action-Value Function)
Reward Function \begin{equation} R_t = \sum_{i=t}^{T} \gamma^{i-t} r_i \end{equation}
其中,$R_t$ 表示在时间 $t$ 的回报值,它是从时刻 $t$ 开始,直到最终状态 $T$ 为止所获得的所有奖励值的累加和。$\gamma \in [0,1]$ 则是一个折扣因子,表示对未来奖励的重视程度。通常,它的取值越接近 1 则越强调未来奖励的重要性。
Action-Value Function
动作价值函数(Action-Value Function)是一个用来衡量智能体在某个状态下执行某个动作后遵循某个策略所能获得的期望长期回报的函数,它反映了不同动作对智能体的优劣。
\begin{equation} Q_{\pi}(s, a) = \mathbb{E}[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) | S_t = s, A_t = a], \end{equation}
这个公式表示了策略 $\pi$ 在状态 $s$ 中采取动作 $a$ 时的价值,即从该状态和动作开始,在采用该策略之后所有未来奖励的总和的期望值。其中, $\gamma$ 表示的是折扣因子( discount factor),用于权衡当前奖励与未来奖励的重要性。
\begin{equation} Q^\star(s,a)=\max_\pi Q_\pi(s,a) \end{equation}
公式3是最优动作价值函数(Optimal Action-Value Function),其用来衡量智能体在某个状态下执行某个动作后遵循最优策略(Optimal Policy)所能获得的最大期望长期回报,它反映了对于不同动作的最佳选择。
打一个比方,在一个游戏中的某个状态下,基于$Q^*(s,a)$函数,向上向左向右移动的action分别会获得:10,29,32分,那么我们基于这个打分,我们应该选择向右移动。
State-Value Function
状态价值函数(State-Value Function)是一个用来衡量智能体在某个状态下遵循某个策略(Policy)后所能获得的期望长期回报(Return)的函数。它反映了不同状态$s$对智能体的重要性
\begin{equation} V_{\pi}(s) = \mathbb{E}[R_{t+1} + \gamma V(S_{t+1}) | S_t = s] \end{equation}
这个公式表示了策略 $\pi$ 在状态 $s$ 上的价值,即从该状态开始,在采用该策略之后所有未来奖励的总和的期望值。同样的,这里的 $\gamma$ 也是折扣因子。
Deep Q-Network (Value-Based)
Deep Q-Network 用神经网络来近似$Q^{\star}(s, a)$。Deep Q-Network 的目标是让神经网络输出的 $Q$ 值尽可能接近 $Q^{\star}$ 值,从而在每个状态下选择能够使长期回报最大化的动作。这可以通过以下损失函数来实现:
\begin{equation} L(\theta) = \mathbb{E}_{s,a,r,s’\sim D}[(r + \gamma \max _{a’}Q(s’,a’;\theta^-) - Q(s,a;\theta))^2] \end{equation}
其中 $s$ 是当前状态,$a$ 是当前动作,$r$ 是当前奖励,$s’$ 是下一个状态。它们都是从经验回放的缓存中随机采样的。$\theta$ 是神经网络的参数,$\theta^-$ 是目标网络(Target Network)的参数,$D$ 是经验回放(Experience Replay)的缓存,$\gamma$ 是折扣因子(Discount Factor)。
DQN损失函数的设计其实用到了Temporal Difference Learning,它根据当前状态和动作的价值函数估计和下一个状态(TD(0))和最优动作的价值函数估计来计算TD误差,然后用这个误差来调整神经网络参数,使得预测值更接近目标值。
基于随机梯度下降(Stochastic Gradient Descent)方法,来更新神经网络的参数的公式如下,其中$N$是batch size,$\alpha$是学习率
损失函数的梯度
$\nabla_\theta L(\theta) = \frac{1}{N}\sum_{i=1}^N\nabla_\theta(y_i - Q(s_i,a_i;\theta))^2 = \frac{2}{N}\sum_{i=1}^N(y_i - Q(s_i,a_i;\theta))\nabla_\theta Q(s_i,a_i;\theta)$
参数更新
$\theta \leftarrow \theta - \alpha\nabla_\theta L(\theta) = \theta - \frac{2\alpha}{N}\sum_{i=1}^N(y_i - Q(s_i,a_i;\theta))\nabla_\theta Q(s_i,a_i;\theta)$
Policy Network (Policy-Based)
Policy Network使用一个神经网络来直接输出给定状态下的动作概率分布。Policy Network的优点是可以处理连续动作空间和高维状态空间,而且可以避免最大化误差的累积。
假设状态空间为$S$,动作空间为$A$,策略函数为$\pi:S\times A\to [0,1]$,表示在状态$s\in S$下选择动作$a\in A$的概率。Policy Network是一个参数化的神经网络,用$\theta$表示其参数,那么$\pi_\theta(s,a)$就是Policy Network的输出。Policy Network的目标是通过学习$\theta$来最大化累积奖励(或者价值函数)。
价值函数有两种形式,一种是状态价值函数,表示在状态$s$下遵循策略$\pi$的期望回报,记为$V_\pi(s)$;另一种是状态-动作价值函数(上文中的),表示在状态$s$下执行动作$a$并遵循策略$\pi$的期望回报,记为$Q_\pi(s,a)$。
状态价值函数和状态-动作价值函数之间的关系为:$V_\pi(s)=\sum_{a\in A}\pi_\theta(a|s)Q_\pi(s,a)$,即在不同策略概率下$Q$的期望。在Policy Network中,我们最大化状态价值函数$V_\pi(s)$(目标函数)
由于需最大化目标函数,我们使用梯度上升法,即沿着策略性能增加的方向更新参数。这就需要计算策略性能关于参数$\theta$的梯度,即对$V_\pi(s)$求$\theta$的偏导
Actor-Critic Methods
Actor-Critic Methods结合了Value-Based Methods以及Policy-Based Methods,其不仅获得了上述两种方法的优点,同时也在一定程度上避免了
- Value-Based:高偏差 (High bias),不能直接得到动作值输出,难以用于连续动作空间
- Policy-Based:高方差(High Variance),训练不稳定,策略收敛困难
它包括两个部分:Actor和Critic。Actor是一个策略网络$\pi_\theta (a|s)$,输入状态,输出动作,主要用来控制策略的运动;Critic是一个价值网络,输入状态或状态-动作对,输出价值函数 $V_w(s)$ 或 $Q_w(s, a)$,可以用来给Actor进行打分。
参考下wangshuseng的note,其整个流程如下:

Conclusion
在本文中,我们学习了RL基本流程与一些关键性概念,包括回报函数(Reward Function),状态价值函数(State-Value Function)以及动作价值函数(Action-Value Function)。同时,我们还介绍了Value-Based Methods以及Policy-Based Methods,更进一步,Actor-Critic Methods结合了两种方案,并获得了相对更优的效果。